Category Theory and C++

Programming is a nice activity. But I had some problems - as a physicist - to be totally satisfied by programming code. My education implied knowlegde of very powerful mathematical topics - analysis, functional analysis, group theory, integration theory, linear algebra and others. So my question was

What is the gap between mathematics and programming?

On the other side I was working over many years in a industrial software development company and I asked myself

Even if I know more about the relation between software development and mathematics, how can I change my company?

Especially, if I look on C++ code, I evolved over the years powerful code migration capabilities. So I ask myself

What can I do inside C++?

For C++ developers it could be a chance to change their view on software development.

After some investigations (it took some years) I found a relation to the lambda calculus (Alonzo Church around 1930) and the combinatory logic (Schönfinkel/Curry around 1920). They invented these formal languages for a better understanding of logic. With the term logic we may connect the question

Is an assumption/hypothesis correct or not.

As a software developer I'm also interested in this question

Is my code correct or not?

Historically it's important to see, that these first formal languages were invented without the existance of computers and the possiblity of code interpretation by a machine. That a computer programm may crash because of mistakes was never - or a long time not - a mathematical option to think about.

It's sometimes difficult to understand the mathematical abstraction levels made in the area of logic. I'm very sure, that it would be possible to describe problems of logic in a way that makes it easier for software developers of today to understand. I'm working in this direction.

This question isn't quit correct. Before we develop code, we need to know what is the topic or the context of the code. Normally a function declaration delivers the hypothesis/proposition and the function body delivers the appropriate code. So the code represents simply a proof, that the function declaration - the specification - is constructible.

Furthermore, the function name has a meaning in the mind of the developer and the code must fit. We are in the area of semantics - human interpretation of a name and the corresponding code depends on human logic.

But what is the meaning of logic - of understanding something?

The complexity of this question can be expressed by another one

Is there a way to let the compiler also check semantics - what is semantics?

Perhaps category theory may help to give an answer by delivering a connection between theories and models/semantics via the basic concept of functors. Very important in this context are types. With types we can get closer to compiler verified semantics.

What I want to do first, is describing a programming style, which is completely generic. In a completely generic world object oriented abstraction is perhaps not so much important and can be replaced completely by (c++ specific) template specializations. This will be the starting point for theories about data and functions.

In general I want to use concepts only if I need them. So I would use object oriented inheritance only if I need it. It's not a question if I like the object oriented paradigma or not.

AI is also a generative way to get code. It translates a natural language prompt into code. Even if the prompt language consists of c++ terms, like developers talk about their problems on e.g. stack overflow, the translation maps human language semantics into code. The question remains if so called boilerplate code really is all the time boilerplate code or is there perhaps also some knowledge inside?

The goal is to fill the gap between software development (writing code) and mathematical logic, looking on the same time to category theory and it's methods of understanding things in a general way.

The technical idea is to derive all elements of programming from a basic generic type definition

template<typename... T>
struct obj;

We will make a difference between objects we want to use in a new language and technical objects, which help us to make the new language working. Helper objects are private with respect to the construction level.

Like in category theory the term object isn't meant as it is used in object oriented programming. For those developers this term is a little bit poisoned.

In the namespace name we define names or symbols

namespace name
{
   struct fun;
   struct data;
}

Now we can introduce function types by

#define FUN(args...) obj<name::fun,args>

template<typename... T>
struct FUN(T...);

and data types by

#define DATA(args...) obj<name::data,args>

template<typename...T>
struct DATA(T...);

The helper macrocs FUN and DATA are working in some cases better than type aliases.

The usability of type aliases is restricted. So we cannot derive template specializations from an alias

//not working
template<>
struct fun<name::sum>;

//works
template<>
struct FUN(name::sum);

On the declaration side te declarations can become very lengthy.

Functions and Data are interpretations (mappings) of the generic type obj - in contrast to object oriented inheritance practises.

This approach leads to lengthy constructions. Technically this is not a problem. But if the goal is to develop a nice to use programming language some additional consideration will be necessary.

Let's now define a function sum, first by defining a new symbol

namespace name
{
   struct sum;
}

Then by making a template specialization

template<>
struct FUN(name::sum)
{
  template<typename A>
  constexpr A operator()(A&& a1, A&& a2);
};

constexpr sum = FUN(name::sum)();

The implementation part of this function (which we want to organize in different files) looks like

template<typename A>
constexpr A FUN(name::sum)::operator()(A&& a1, A&& a2)
{
  return a1 + a2;
}

//application using the constexpr object
int main()
{
  return sum(1,2);
}

With c++-20 we can improve the situation by adding a constraint already at the function definition level

template<typename A>
requires numeric<A>
A operator()(A&& a1, A&& a2)
  ...

Here we have a link to category theory. Better than a numeric constraint would be a monoid constraint. A monoid is more general than a numeric constraint, it includes also strings and similar types. Such things will be discussed later.

In general it must be a strategic goal to enrich the specification side. We want to know as much as possible by reading the specification of a function only.

The way of defining functions according to the definition above has the advantage, that those functions are first class objects - simply, they represent a type - not only a signature. Also lambdas in c++ are shortcuts to such a function with only one call operator. In contrast to lambdas, the provided function definition is more flexible. Espacially we can write typed polymorphic functions in a very elegant way.

In general we transport most dependencies mainly via implentation code. So we can use pure declarations in pure headers - denoted by the hpp file extension and implementations in implementation files - denoted by the hxx file extension. Thus hpp will be included in the corresponding hxx files, which themselves should only be used in object sources (where the compiler creates an obj/o file) denoted by the cxx file extension.

In this section I try to extend the data object by introducing a context and a list of allowed constructors. I follow here the idea of datatypes in functional languages. This approach avoids inheritance coupling we typically get in object oriented code

template<typename C, typename... A>
struct DATA(C,A...)
{
  template<typename X>
  requires IsOneOfCtrTypes<X,C,A...> 
  obj(X&& x);

  ~obj();

  void* ctr;
  const unsigned index;
};

source	description
git	repository
cat_tl.hpp	typelist
cat.hpp	basics
cat.hxx	– implementations
cat_data.hpp	polymorphic data
cat_data.hxx	– implementations

To get a data object, we need an allowed contructor object (IsOneOfCtrTypes - defined in the details - a typelist related function). The anonymous constructor pointer is stored in the ctr member. The index within the typelist of allowed constructors is stored in the index member. The index member will be used later for an upcast to the real constructor object. Such an upcast must be done by the destructor to destroy the concrete ctr resources and by the polymorphic function application, which applies a polymorphic function - polymorphic over the constructor objects - on a data object.

In category theory such polymorphic objects are called sums.

Such a construction is known in c++ as a variant data type in combination with the visitor pattern. If we would look on a polymorphic data type as a generalization of normal data, than we can understand the visit function of the visitor pattern simply as a generalization of function application in the context of polymorphic data types. Furthermore it's necessary to provide a generalized definition of the term function, which is appropriate in this context.

The first template parameter C defines a context and the remaining template arguments may help to specialize the context. So a context shape may define types - rectangle, square, and circle - a list of types, from which we can construct allowed constructor objects.

Let's start to define a context to be derived from obj

namespace name
{
  struct ctx;
}

#define CTX(args...) obj<name::ctx,args>

template<typename T,typename... A>
struct CTX(T,A...)
{
  using types = tl<>;
};

//shortcut
template<typename T, typename... A>
using ctx_types = typename ctx<T,A...>::types;

Undefined here is tl, which represents a typelist - defined here | cat_tl.hpp |. The context is defined by a type T and potential additional subcontexts are defined by additional type arguments A…. By default, the context related typelist is empty.

Without subcontexts we can only construct abstract datatypes (ADT) and with it we can define general abstract datatypes (GADT). These terms are wellknown in functional languages.

The typelist tl allows to specify an allowed list of constructors. Such a constructor can be defined in the following way

namespace name
{
  struct ctr;
}

#define CTR(args...) obj<name::ctr,args>

template<typename C,typename D, typename... A>
requires (is_element_of<D,ctx_types<C,A...>>())
struct CTR(T,D,A...);

This definition tells us, that the constructor belongs to a context and the constructor name is an element of the context typelist.

As an example, let's construct a shape datatype

namespace name
{
  struct shape;
  struct rectangle;
  struct circle;
  struct square;
}

template<>
struct ctx<shape>
{
  using types = tl<name::square,name::rectangle,name::circle>;
};

template<>
struct CTR(name::shape,name::circle)
{
  double r;
};

template<>
struct CTR(name::shape,name::rectangle)
{
  double a;
  double b;
};

template<>
struct CTR(name::shape,name::square)
{
  double a;
};

As a function, which is polymorphic with regards to these constructors, we may define

namespace name
{
  struct perimeter;
}

template<>
struct FUN(name::perimeter)
{
  const double pi = 3.14;

  constexpr double operator()(const CTR(name::shape,name::circle)& c) const
  {
    return 2*pi*c.r;
  }

  constexpr double operator()(const CTR(name::shape,name::square)& s) const
  {
    return 4*a;
  }

  constexpr double operator()(const CTR(name::shape,name::rectangle)& r) const
  {
    return 2*a*b;
  }
};

constexpr auto perimerter = FUN(name::perimeter);

This constexpr function object is always constructible. The constexpr operators only if they use only constexpr function calls.

A shape object can now be constructed via

DATA(name::shape) shape(CTR(name::shape,name::circle){5.0});

We can also apply the perimeter function to an ctr object

auto p = perimeter(CTR(name::shape,name::circle){5.0});

To be able to apply the polymorphic function perimeter to the shape data object, some preparations are necessary.

Normally in c++ a function f is applied to a value x by a call operator (open-close parenthesis)

auto y = f(x)

Formally we can replace such an expression by using an fictional operator

auto y = f <<a>> x;

For other function application situations we can now generalize value applications by appropriate operators. So the shape object can then be applied to the perimeter function (from the last section) with a data application operator

auto p = perimeter <<da>> shape;

If we would have such an operator, then we can even extend the perimeter function by an redirector call

template<>
struct FUN(name::perimeter)
{
  tmplate<typename D>
  requires Data<D,name::shape>
  constexpr double operator()(D&& d) const
  {
    return (*this) <<op::da>> fwd(d);
  }

  ...
};

This construction takes advantage of universal references together with a Data constraint, which restricts the template parameter D to be of the form

template<typename C, typename... A>
struct data<C,A...>

The macro fwd garantees what we understand as perfect forwarding of the universal reference function parameter d.

Universal references together with perfect forwarding is very powerful possibility in working with c++ templates, because it simplifies codegeneration with respect to all value categories, which we have typically in c++.

With such an operator extension we can apply the perimeter function in the two different ways

auto x = perimerter <<op::a>> shape;

//or

auto x = perimeter <<op::da>> shape;

An example can be found here

source	description
git	repository
testdataapplication.cpp	testcode

This is a very fruitful generalization on function application. We will see later, that there are some other very interesting function application concepts, which we can also express by an operator.

Operators are only a shortcut to unary or binary function calls. The main advantage of operators is, that we don't need any parenthesis. Perhaps not less important - operators may represent abstractions.

We can read the constraint Data<D,name::shape> mathematically as

For all types D, which have a valid form DATA<D,name::shape> there exists a function perimeter.

This is not the end of the constraint story.

The question is, if we can give a more precise idea of what a perimeter result is? A double is a very poor semantic information. The semantics is given by the function name in this example. Perhaps we can construct a relation between the function name and the function's return type. This is in principle possible, because the function name is a compiler known name.

As an introduction it's ok.

A little bit in touch with category theory we get by defining an operator, which realizes the idea of an exponential transpose

auto p = (perimeter <<op::ta>> shape)();

A clearer sight on the behaviour we get by looking at another example - a binary multiplication

auto x = (multi <<op::ta>> 2)(3);

//or

auto multi2 = multi <<op::ta>> 2;
auto x = multi2(3);

Using std::bind we could write

auto x = bind(multi,2,_1)(3);

//or

auto multi2 = bind(2,_1);
auto x = multi2(3);

The actual transpose operation always works from the left to the right, without any positional parameter support.

In the context of functional programming languages we talk about currying. Sometimes currying is directly supported by programming languages, this means

multi(a,b) <==> multi(a)(b)

In c++ such an equivalence isn't constructible. From the perspective of category theory such an equivalence isn't necessary.

Two helper operators can be delivered. The first one transforms a lambda into a function (the plus sign is perhaps not the best choice)

auto f = +[](int a, int b) { return a + b; };
auto s = f(2,3);
//or
auto s = f <<op::ta>> 2 <<op::a>> 3;

We cannot apply a binary function to a value. For this a exponential transpose is required.

The second one transforms a function into an exponential transpose

auto multi = +[] (int e, int f) {
  return e*f;
};

auto m = (~multi) <<op::a>> 2 <<op::a>> 3;

The transformation of a binary function to a exponential transpose, returns a function with one argument, which returns a function of the remaining arguments.

source	description
git	repository
catoperator.hpp	operators
catoperator.hxx	– implentations
catapplication.hpp	normal function application
catapplication.hxx	– implementations
cattranspose.hpp	normal function application
cattranspose.hxx	– implementations
catlambda.hpp	lambda transformation
catlambda.hxx	– implementations
catdataapplication.hpp	polymorphic data application
catdataapplication.hxx	– implementations
testtranspose.cpp	test code

Because the possibilities to define operators in c++ is very limited, an alternate approach will be described in the following technical section.

The binary operator concept used here is contructed by a pair of operators – << and >>. The first operator << captures a function on the left and the application function on the right into an helper object, and the second operator >> applies the captured function to the data on the right using the captured application function. So we get

auto x = fn <<apply>> data;

//or

auto x = apply(fn,data);

The simplest version of an apply function would be

struct obj<name::function,name::apply>
{
  template<typename F, typename D>
  decltype(auto) operator()(F&& f, D&& d)
  {
    return fwd(f)(fwd(d));
  }
};

A simple definition of the operators may be given by

template <typename F, typename O>
requires Function<O>
constexpr decltype(auto) operator<<(F&& f, O&& o)
{
  return op::capture<O,F>{fwd(o),fwd(f)};
}

template<typename C, typename A>
constexpr decltype(auto) operator>>(C&& c, A&& a)
{
  using F = decltype(fwd(c).f);
  if constexpr (std::is_lvalue_reference<F&&>::value) {
    return fwd(c).o(fwdl<C>(fwd(c).f),fwd(a));
  } else {
    return fwd(c).o(std::move(fwd(c).f),fwd(a));
  }
}

So the operator type O should be a function. Together with the following capure helper we get an impression how it works

template<typename O, typename F>
struct capture
{
  O o;
  F f;
};

Such a construction is intended to be used only in a reference context. Copying data must be avoided in general. This aspect has a high impact on the programming style.

source	description
git	repository
catoperator.hpp	operators
catoperator.hxx	– implentations
catapplication.hpp	normal function application
catapplication.hxx	– implementations
cattranspose.hpp	normal function application
cattranspose.hxx	– implementations
catdataapplication.hpp	polymorphic data application
catdataapplication.hxx	– implementations
testtranspose.cpp	test code

Our language consists at the moment on the following elements

element	description
functions	obj<name::fun,…>
data	obj<name::data,…>
data context	obj<name::ctx,…>
data constructors	obj<name::ctr,…>
operators
application operator
transpose operator	~
transpose application operator	f x <=> ~f x
data application operator
namespace cat	base namespace
sub namespace name	namespace for simple names
sub namespace op	namespace for operator shortcuts

Essential helpers are

A name is simply a type. If a name is needed and there isn't an appropriate type available then a new one can be put into the namespace name. Such names normally need not to have a body.

The perfect forwarding macro fwd is used systematically in the context of universal references - even it is not necessary in some cases.

Guidelines have a similar effect on codeing like the development of a new language. They are usage restrictions of the complete language to a subset with the goal to avoid programming mistakes. Ideally such a restriction can be checked automatically.

The idea to save container data into a polymorphic value type, makes the situation too complicated. A const reference type seems to be powerful enough. The strategy must be to avoid data copies as often as possible.

Why loops are a problem? Loops are a problem because of the body, which may contain potential programming errors. But if we consequently replace the loop body by a separated body function (perhaps a lambda), the problem is still in that function and the code may become perhaps worse to read

std::list<int> test_function(std::list<int> l)
{
  std::list<int> rl;

  for(auto& e: l) {
    rl.emplace_back(e*e);
  }
}

can be transformed to

std::list<double> test_function(std::list<int> l)
{
  std::list<double> rl;

  auto one_third = [&rl] (int e) {
    rl.emplace_back(e*0.33333);
  };

  for(auto& e: l) {
    one_third(e);
  }

  return rl;
}

In the C++ standard we will find functional structures for avoiding explicite looping

std::list<double> test_function(std::list<int> l)
{
  std::list<double> rl;

  auto one_third = [&rl] (int e) {
    rl.emplace_back(e*0.33333);
  };

  std::for_each(l.cbegin(), l.cend(), one_third); 

  return rl;
}

After a look at the code, can I deliver an argument, why we should do this? My answer is - at the moment I don't have one. But because I want to create a new language and we need some words of this language to construct something we can compare with the old language, I start with a perhaps silly example. This is an journey of construction experiments. So proclaiming a problem avoiding loops is at first a pseudo motivation and finally an introduction drug.

Another approach would be is to write 10 pages of theoretical arguments for a new language, which nobody would read.

Let's now go a different direction and let's look on the functor concept coming from category theory

namespace cat
{
  template<typename T>
  struct functor;

  template<typename T>
  struct functor<std::list<T>>
  {
    template<typename F, typename A>
    decltype(auto) operator()(F&& f, const std::list<A>& l)
    {
      using type = decltype(fwd(f)(std::declval<A>()));

      std::list<type> rl;

      auto x = [&rl,ff=fwd(f)](const auto& e) {
        rl.emplace_back(ff(e));
      };

      std::for_each(l.cbegin(), l.cend(), x);

      return rl;
    }
  };
}

The template functor is said here to be an interpretation and especially in this case an interpretation of a list. The macro fwd helps to shorten forwardings in the area of universal references. For the moment lets state

An interpretaton is a mapping of a type to another interpretation type.

Next take a look on the code

std::list<double> test_list_functor(std::list<int> l)
{
  auto one_third = [] (int e) {
    return e*0.33333;
  };

  return cat::functor<decltype(l)>()(one_third,l);
}

The functor selector decltype(l) is not a perfect selector, because l stands for a value category - const or reference or both together. Later I define an additional helper tp to extract the type from the value category.

It's perhaps clear, that such container iterations can be generalized, so that the looping mechanism we only needed to be implemented at one place.

But this is not enough. Important seems to me, to express the relation to an arithmetic calculation by an operator. First take a look on the wish

std::list<double> test_list_functor(std::list<int> l)
{
  auto one_third = [] (int e) {
    return e*0.33333;
  };

  return one_third <<fa>> l;
}

In functional languages we can find a \(\lt{}$\gt{}\) operator. In C++ our possiblities to define operators are limited. I'm trying to circumvent this by using an approach found on different sites in the web, looking for "custom operators in C++". But what would the \(\ll{}a\gg{}\) operator express - in contrast to \(\ll{}fa\gg{}\) - simply

std::list<double> test_function(int i)
{
  auto one_third = [] (int e) {
    return e*0.33333;
  };

  return one_third <<a>> i;
}

So

\(one\_third \ll{}a\gg{} i\)

is simply

\(one\_third(i)\).

Using an operator instead of parenthesises is a very important method to express the application of a function to a value in functional languages. So let's apply the function one_third two times, using the application operator

std::list<double> test_function(int i)
{
  auto one_third = [] (int e) {
    return e*0.33333;
  };

  return one_third <<a>> one_third <<a>> i;
}

This looks much more elegent and readable than

std::list<double> test_function(int i)
{
  auto one_third = [] (int e) {
    return e*0.33333;
  };

  return one_third(one_third(i));
}

I think functional programmers wouldn't like so much their language without having these operators.

We can see, that the operator \(\ll{}fa\gg{}\) is an extension of an ordinary function application, where the function is applied to a functorial value. And functorial means, that for a given value type exists a functor interpretation.

If we would generate a new function via the functor operator instead of directly applying the function to the value, we would get the following situation

std::list<double> test_list_functor(std::list<int> l)
{
  auto one_third = [] (int e) {
    return e*0.33333;
  };

  return cat::functor<decltype(l)>()(one_third) <<a>> l;
}

We can directly apply the value to the new generated function. This approach of the functor implementation looks like

namespace cat
{
  template<typename T>
  struct functor<std::list<T>>
  {
    template<typename F>
    constexpr decltype(auto) operator()(F&& f) const
    {
      return [ff=fwd(f)] (auto&& l) {
        using type = decltype(ff(std::declval<decltype(*l.begin())>()));

        std::list<type> rl;

        for(auto& e: l) { rl.emplace_back(ff <<a>> e); }

        return rl;
      };
    }
  };
}

Function generation code can always declared as constexpr. Perhaps it is surprising - because of the auto in the lambda declaration - it is possible to do the following

std::list<double> test_function(std::list<int> l)
{
  auto one_third = [] (int e) {
    return e*0.33333;
  };

  auto list_one_third = cat::functor<std::list<int>>()(one_third);

  return list_one_third <<a>> l;
}

The lambda is a shortcut to an object with one call operator, list_one_third represents the object, not directly the operator method. The template resolution is done only at application time. Instead of using a lambda, we can make it more explicit, using a fun object

namespace cat
{
  template<typename...>
  struct fun;

  template<typename T, typename F>
  struct fun<std::list<T>,F>
  {
    template<typename A>
    const decltype(auto) operator()(A&& a) const
    {
      using type = decltype(f(std::declval<decltype(*a.begin())>()));

      std::list<type> rl;

      for(auto& e: fwd(a)) { rl.emplace_back(f <<a>> e); }

      return rl;
    }

    const F f; 
  };

  template<typename T>
  struct functor<std::list<T>>
  {
    template<typename F>
    constexpr decltype(auto) operator()(F&& f) const
    {
      return fun<std::list<T>,F>{fwd(f)};
    }
  };
}

The lambda replacement captures the function object in a member variable. The fun interpretation or longer function is another interpretation, which is more fundamental then the functor interpretation. The next section will take a closer look on functions.

Like a functor interprets a type - a function introduced in this section will also interpret types.

namespace cat
{
  template<typename...>
  struct fun;
}

To specify a function we must introduce a name as a type

namespace cat::name
{
  struct sum;
}

Now we can give the term sum an interpretation

namespace cat
{
  template<>
  struct fun<name::sum>
  {
    template<typename A>
    A operator()(A&& x, A&& y)
    {
      return fwd(x) + fwd(y);
    }
  };
}

In this context name introduction is perhaps the better term than type forwarding. As a name, a type is fully specified.

This interpretation of a function is closely related to a lambda, which isn't different from such a function with one call operator. Our function definition is more flexible, because we can build polymorphic functions

namespace cat
{
  template<>
  struct fun<name::perimeter>
  {
    double operator()(const circle& c)
    {
      return 2 * pi * c.r;
    }

    double operator()(const rectangle& r)
    {
      return 2 * (r.a + r.b);
    }
  };
}

We need these functions to introduce the next language element - the polimorphic data type. This will be done in one of the following sections.

Let's use the fun concept to introduce a lambda using a deduction guide

namespace cat
{
  namespace name
  {
    struct lambda {};
  }

  template<typename F>
  struct fun<name::lambda,F>
  {
    fun(F&& f, name::lambda) : m_f(fwd(f)) {}

    F m_f;
  };

  template<typename F> fun(F&&) -> fun<name::lambda,F>;
}

Now we can write

auto f = fun{[](){}};

If it is really a good idea, we will see later. For the moment I want to provide a helper operator - the plus sign, to make the lambda transformation easier

namespace cat
{
  template<typename F>
  decltype(auto) operator+(F&& f)
  {
    return fun(fwd(f));
  }
}

Another thing we can do with a function, we can look on a functor as a special function

namespace cat
{
  namespace name
  {
    struct functor;
  }

  template<typename... T>
  struct fun<name::functor,T...>;

  template<typename... T>
  using functor = fun<name::functor,T...>;
}

At this point we can also make the code more general, if we look on a function as special object

namespace cat
{
  namespace name
  {
    struct function;
  }

  template<typename... T>
  struct cat_object;

  template<typename... T>
  using fun = cat_object<name::function,T...>;
}

In principle such an approach is possible, but at this stage it would be perhaps over structured. So we can take it if we need it.

To make generic programming more powerful universal references and perfect forwarding were invented. This mechanism allows us to provid one implementation of a function for several purposes - in the context of value categories. Very important to make universal references working is to use the general form

template<typename T>
MyReturnType MyFunction(T&& t)
{
  ...
}

Sometimes this general form is too general in certain situations. With C++20 we can now call on concepts to specify additional constraints. Before C++20 it was not so handy by using sfinae - espacially if variadic templates are used.

So I'm using C++20 concepts and perfect forwarding very systematically. And this is very important, because the problems, which may occur in providing fundamental solutions of functional programming with generic C++ code, are sometimes very difficult to understand and to solve.

Beside the problem of forwarding simple data, forwarding of container data - like the elements of a list, must be regarded. Because such data is always bound to a variable, we get always lvalue references to these data elements. The interpretation of container elements depends on the value category of the container itself. So if a container has the value category of a rvalue, the value category of a container element should also be interpreted as such. This consideration leads to the following helper construction

namespace name
{
  struct forward_like;
}

template<ttypename T>
struct fun<name::forward_like>
{
  template<typename U>
  constexpr auto&& operator()(U&& u)
  {
    constexpr bool is_adding_const = std::is_const_v<std::remove_reference_t<T>>;

    if constexpr (std::is_lvalue_reference_v<T&&>)
    {
        if constexpr (is_adding_const)
            return std::as_const(x);
        else
            return static_cast<U&>(x);
    }
    else
    {
        if constexpr (is_adding_const)
            return std::move(std::as_const(x));
        else
            return std::move(x);
    }
  }
};

template<typename T>
using forward_like = fun<name::forward_like,T>;

The forward_like function is part of the c++23 standard. The code above is simply an aligned copy of the "a possible implementation" found in the C++ reference pages.

The whole theory on avoiding loops can be express in an abstract diagram

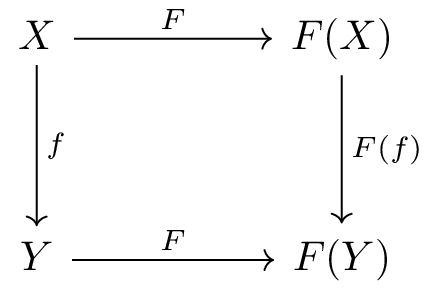
The meaning of the different arrow types is - they cannot be composed. The function f transforms a value of type A to a value of type B. The type transformation T maps a type value A to the type value X and the type value B to the type value Y. If we use value declarations, f can be defined as

\(f: (x:X) \rightarrow (y:Y)\)

and the type mapping T we can define as

\(T: (A:Type) \rightarrow (X:Type)\)

In our template language C++ we may write

\(X = T\langle{}A\rangle\)

But a language like Idris, where types are first class objects, we can write down this relation as a normal function

\(X = T(A)\)

An alternative way to describe a function is the exponential style

\(f: B^A\)

The superscript A denotes the type of the function argument - B represents the return type of the function.

This is what we have in the functor picture \(F_T(f)\), that is

\(F_T: B^A \rightarrow T\langle{}B\rangle{}^{T\langle{}A\rangle{}}\)

Every binary function

\(f: A \otimes B \rightarrow C\)

can be expressed by two unary function calls

\(f(a,b) = \overline{f}(a)(b)\)

Here is \(\overline{f}\) the exponential transpose

\(\overline{f}: A \rightarrow C^B\)

With an application \($\) operator we can also write

\(f \ $\ (a,b) = \overline{f} \ $\ a \ $\ b\)

But what happens if we try to extrapolate this situation to an unary function

\(f \ $\ a = (\overline{f} \ $\ a)()\)

The exponential transpose takes a parameter and returns a function, which needs no argument to be executed. We can say

\(\overline{f} \ $\ a = \hat{f}_{f(a)} \qquad with \qquad \hat{f}_{f(a)}() = f(a)\)

In books on category theory the relation between a binary function and its exponential transpose is expressed by an evaluation function

\(eval: C^B \otimes B \rightarrow C\)

with

\(f = eval \cdot (\overline{f},\identity{})\)

We can now apply on both sides a value \((a,b):A \otimes B\)

\(f(a,b) = eval \cdot (\overline{f},\identity{})(a,b) = eval(\overline{f}(a),b)\)

which can be reduced to the already known formula

\(f(a,b) = \overline{f}(a)(b)\)

Our type based category seems to support exponentials obviously, because we can always construct them. Such a category is a cartesian closed category (CCC).

Details can be read in books on category theory. Now, first a sidestep follows - custom operators.

The idea is to contruct a new operator using the existing operator pair \(\ll\) - \(\gg\). This will only work if we use a capture object between.

So first we need a strategy object and then a the capture object:

namespace cat::op
{
  const struct a_t {} a;
  const struct ta_t {} a;
  const struct fa_t {} a;
  const struct fta_t {} a;

  template<typename C, typename V>
  struct capture
  {
    V v;
  };
}

The \(\ll\) operator captures the function object v and also the capture strategy type - the type C. Beside the application operator I also want to provide transpose operators, which apply a value and returns the transpose of a function. Dependend on the capture strategy type the behaviour can be controlled:

namespace cat
{
  template <typename F, typename O>
  decltype(auto) operator<<(F&& f, const O&)
  {
    return op::capture<O,F>{fwd(f)};
  }

  template<typename F, typename G>
  decltype(auto) operator>>(F&& f, G&& g)
  {
    if constexpr (is_op<op::a_t,F>) {
       return fwd(f).v(fwd(g));
    }
    if constexpr (is_op<op::ta_t,F>) {
       return ~fwd(f) <<op::a>> fwd(g);
    }
    if constexpr (is_op<op::fa_t,F>) {
      return functor<util::clear_type<G>,
                     name::application>()(fwd(f).v)(fwd(g));
    }
    if constexpr (is_op<op::fta_t,F>) {
      return functor<util::clear_type<G>,
                     name::transpose()(fwd(f).v)(fwd(g));
    }
    //This case should never happen - taking first simply a throw
    throw 1;
  }
}

The operator strategy detection is implemented in the following way

namespace detail
{
  template<typename A, typename C>
  struct is_op : std::false_type {};

  template<typename A, typename X>
  struct is_op<A, op::capture<A,X>> : std::true_type {};
}

template<typename A, typename C>
static constexpr bool is_op =
  detail::is_op<A,util::clear_type<C>>::value;

The helper construction clear_type, which reduces the *value category" to a type expression is implemented this way

namespace cat::util
{
  template<typename T>
  struct clear_type_decl
  {
    using T1 = typename std::remove_reference<T>::type;
    using T2 = typename std::remove_pointer<T1>::type;
    using type = typename std::remove_const<T2>::type;
  };

  template<typename T>
  using clear_type = typename clear_type_decl<T>::type;
}

Finally a test function shows how to use all of it

double test_list_functor(int i)
{
  auto one_third = +[] (int e) {
    return e*0.33333;
  };

  return one_third <<op::a>> i;
}

The + sign generates a lambda into a fun<lambda> - see the introduction of the lambda function in the functions as interpretation section.

In the case of a binary function, we need the transpose of this function. If we provide the transpose generator as the operator ~, the example code could look like this

int test_list_functor(int a, int b)
{
  auto multi = +[] (int e, int f) {
    return e*f;
  };

  return ~multi <a> e <<op::a>> f;
}

The transpose operator ~ returns a transpose function, which is defined as

namespace cat
{
  namespace name
  {
    struct transpose {};
  }

  template<typename F, typename A>
  struct fun<name::transpose, F, A>
  {
    template<typename... X>
    constexpr decltype(auto) operator()(X&&... x) const
    {
      return f(a,fwd(x)...);
    }

    const F f;
    const A a;
  };

  template<typename F>
  struct fun<name::transpose,F>
  {
    const F f;

    fun(F&& _f, name::transpose)
      : f(fwd(_f)) {}

    template<typename A>
    constexpr decltype(auto) operator()(A&& a) const
    {
      return fun<name::transpose,F,A>{f,fwd(a)};
    }
  };

  template<typename F> fun(F&&,name::transpose)
    -> fun<name::transpose,F>;

}

With the transpose application operator we can save an operator call

int test_list_functor(int a, int b)
{
  auto multi = +[] (int e, int f) {
    return e*f;
  };

  return multi <<ta>> e <<a>> f;
}

Every step of this evolution can be tested via the sourcecode from the git repo.

Instead of writing loops we want to apply a function on the container elements

decltype(auto) my_fun()
{
  auto f = [](int i) { return double(i/2); };
  std::list l{1,2,3,4,5};

  return f <<fa>> l;
}

and get back a container with elements of the result type of that function. This is what the concept of a functor means to be. But a functor isn't restricted to container types. Type encapsulation is the main aspect which can be handled in general by a functor.

For the practical application of functor operations, the availability of operators is important. The operator allows to plugin new functor definitions without changing the general usage via the operator.

Function application in the functor context is an extension of normal function application, which also can be expressed via an operator.

Beside values, function application may return the transpose of the function, where the applyed value is captured. The different application strategies can be chosen by appropriate operators.

The next goal is to develop the concept of polymorphic datatypes. Again the interpretation aspect plays the main role in this area.

In an object oriented programming style distinguishing between functions and data makes not so much sense, because the struct or the class represents both. My position here is similar but not the same. Structs and classes represent types and both functions and data are types. Because we can recognize a function by an interpreted fun template, we can do the same with data. Asking how functional languages are dealing with data, I give data structures the interpreter name ctr, which should be the shortcut for data constructor.

If we would say

struct circle
{
  double r;
};

We could say, that anything, which isn't a fun specialization is data. Better it seems for me to make it explicit by introducing data and data constructor interpretations

namespace cat
{
  template<typename T>
  struct ctr;

  namespace name
  {
    struct circle;
  }
}

using namespace cat;

template<>
struct ctr<name::circle>
{
  double r;
};

Now it's clear – it's data. Perhaps it makes sense at this point to introduce also a context

namespace cat
{
  namespace name
  {
    struct shape;
    struct circle;
  }

  template<typename, typename>
  struct ctr;
}

using namespace cat;

template<>
struct ctr<name::shape,name::circle>
{
  double r;
};

This looks a little bit like inheritance - but only a little bit. We can now also use the name circle in different contexts

namespace cat
{
  namespace name
  {
    struct grouping;
  }
}

using namespace cat;

template<>
struct ctr<name::grouping,name::circle>
{
  std::list<std::string> names;
};

The first application of these data structures may be a perimeter function

namespace cat::name
{
  struct perimeter;
}

using namespace cat;

template<>
struct fun<name::perimeter>
{
  double operator()(const ctr<name::circle>& c)
  {
    return 2 * pi * c.r;
  }

  double operator()(const ctr<name::rectangle>& r)
  {
    return 2 * (r.a + r.b);
  }
};

Comparing this situation with pattern matching of constructors in functional languages we can also write

using namespace cat;

template<>
struct fun<name::perimeter>
{
  template<typename T>
  double operator()(const ctr<name::shape,T>& t)
  {
     if constexpr (std::is_same<T,name::circle>::value) {
        return 2 * pi * t.r;

     } else if constexpr (std::is_same<T,name::rectangle>::value) {
        return 2 * (t.a + t.b);
     } else {
        std::runtime_error("Missing implementation");
     }
  }
};

At this point we can do a little bit more. We can associate a list of types to a context type and then we allow the construction of data types only for the defined typelist

namespace cat
{
  namespace type
  {
    template<typename... T>
    struct list;
  }

  namespace name
  {
    struct rectangle;
    struct cuircle;

    struct shape
    {
      using types = type::list<circle,rectangle>;
    };
  }
}

Again I must be consequent. The structure shape should be a context as a new language element

namespace cat
{
  template<typename>
  struct ctx
  {
    using types = type::list<>;
  };

  namespace name
  {
    struct shape;
  }
}

using namespace cat;

template<>
struct ctx<name::shape>
{
  using types = type::list<name::circle,name::rectangle>;
};

In the next step I want to check, if the data constructor type is valid. This means, that the data subtype must be in the typelist specification of the context.

namespace cat
{
  template<typename T>
  using ctx_types = typename ctx<T>::types;

  template<typename T,typename D, typename... A>
  requires (*fun<name::type::is_element_of,D,ctx_types<T>>())
  struct ctr;
}

using namespace cat;

template<>
struct ctr<ctx<name::shape>,name::circle>
{
  double m_r;
};

So, how does the is_element_of looks like. Some insights into typelists are necessary.

A typelist simply represents a list of types. A ctr::list will be provided later as a polymorphic data type. To avoid the introduction of a new language element the typelist will be defined here as a data specialization

namespace cat
{
  namespace name
  {
    struct typelist;
  }

  template<typename... A>
  struct data<name::typelist,A...>
  {};

  template<typename... A>
  using typelist = data<name::typelist,A...>;
}

This typelist is a data type without any constructor. If this really makes sense, or if this is a too pedantic approach to do this - I don't know. But it is possible to do it.

For tagging purposes it's allowed to instantiate a typelist, without the risk of any resource allocation.

A typelist, as any list, has two fundamental parts - the first element

namespace cat
{
  namespace detail
  {
    template<typename L>
    struct first;

    template<typename T, typename... TT>
    struct first<typelist<T,TT...>>
    {
      using type = T;
    };
  }

  template<Typelist L>
  using first = typename detail::first<L>::type;
}

and the tail

namespace cat
{
  namespace detail
  {
    template<typename L>
    struct tail;

    template<typename T, typename... TT>
    struct tail<typelist<T,TT...>>
    {
      using type = typelist<TT...>;
    };
  }

  template<Typelist L>
  using tail = typename detail::tail<L>::type;
}

Type aliases are helping to avoid to write always typename-type constructions, and they give us the feeling of a type function.

The concept Typelist allows us to restrict this definition of the first and the tail type functions to typelists. It's defined as

namespace name
{
  struct is_list;
}

template<typename L>
struct fun<name::is_list,L>
{
  constexpr bool operator()() const
  {
    return false;
  }
};

template<typename... T>
struct fun<name::is_list,typelist<T...>>
{
  constexpr bool operator()() const
  {
    return true;
  }
};

template<typename L>
concept Typelist = fun<name::is_list,L>()();

Instead of producing a static value I'm using here a constexpr call operator and also the fun template language element. I'm doing so, to increase the impression, that all is about functions, which reflects the spirit of category theory (take a look on Awodeys Book on Category Theory as an example - listed in the references - the online available version).

The size of a typelist may also be of interest

namespace cat
{
  namespace name
  {
    struct size;
  }

  template<typename... T>
  struct fun<name::size,typelist<T...>>
  {
    constexpr std::size_t operator()() const
    {
      return sizeof...(T);
    }
  };
}

Again, this is also a fun specialization together with a constexpr call operator.

For the desired is_element_of function let's first calculate the index of a type in the list – if available

namespace cat
{
  namespace name
  {
    struct index_of;
  }

  template<typename T, std::size_t I>
  struct fun<name::index_of,T,typelist<>,std::integral_constant<std::size_t,I>>
  {
    constexpr std::size_t operator()() const
    {
      return I;
    }
  };

  template<typename T, typename L, std::size_t I>
  struct fun<name::index_of,T,L,std::integral_constant<std::size_t,I>>
  {
    constexpr std::size_t operator()() const
    {
      return fun<name::util::is_same,T,first<L>>()()
        ? I
        : fun<name::index_of,T,tail<L>,std::integral_constant<std::size_t,I+1>>()();
    }
  };

  template<typename T, typename L>
  struct fun<name::index_of,T,L>
  {
    constexpr std::size_t operator()() const
    {
      return fun<name::index_of,T,L,std::integral_constant<std::size_t,0>>()();
    }
  };
}

If no match is found, the empty list must be handled, here by setting the result to an exceptional value, which is the size of the typelist, which is equal to the max index plus one.

Now it's time to provide the tl_is_element_of function, which translates the numeric index value into a boolean one.

namespace cat
{
  namespace name
  {
    struct is_element_of;
  }

  template<typename T, typename L>
  struct fun<name::is_element_of,T,L>
  {
    constexpr bool operator()()
    {
      return fun<name::size,L>()() > fun<name::index_of,T,L>()();
    }
  };
}

The quint essence of this work is an universal quantifier, which tells us, that for any type, which exists in the typelist of the context, a data constructor is allowed. The data constructor definition looks now like this

namespace cat
{
  template<typename>
  struct ctx
  {
    using types = typelist<>;
  };

  template<typename T>
  using ctx_types = typename ctx<T>::types;

  template<typename T,typename D, typename... A>
  requires (fun<name::is_element_of,D,ctx_types<T>>()())
  struct ctr;
}

The introduction of the term universal quantifier as a property of a data constructor element is nice. Perhaps it is a good opportunity to make some simple notes on logic.

What is logic? A very fundamental question. I'm not the person who should give a definition of logic here. But I know, that logic has to do with the underlying language. Within this language we describe first basic objects and then some construction principles, which describe how to construct more complex objects using these basic objects. Because the more complex objects behave like the basic objects, we can apply the construction principles also to this more complex objects. This way a recursive language definition is developed.

Combining things to more complex things is the area of operators. In classical logic we have operators like \( \land{}, \lor{}, \neg{}, \implies \).

First, the mathematicians started with a language, which was derived from a natural language like english. Then formal languages became of interest, like the lambda calculus or the combinator logic. Today we speak about homotopy type theory or quantitative type theory and perhaps there are other approaches.

The motivation behind the wish, to use a formal language for logical purposes, is to construct proves by programs. Because logical proves may be very complex and thus difficult to manage by persons without a high risk of making mistakes.

Types - in constrast to sets - seem to play an important role in such newer approaches to make logic. In our case a type is simply a name, which can be make known to the compiler. And the generic template engine of C++ allows to do things with these types - especially types may be templated, or type functions.

So we have a relation beween propositions and types and type functions (templated types) and predicates. A resolved predicate is then a proposition - or here a type. Using predicates we have the problem, that not all input parameters (also types) are producing valid result types. A result type is valid if we can produce a value of this type - or a type is valid if a value is constructible.

On the specification side we define now a set of types to be valid as input types. This restriction to a set of usable types can be interpreted as an universal quantifier in mathematics. In C++ it looks like

template<typename R, typename T>
requires "T-is-an-element-of-a-certain-set-of-types"
          &&
         "R-is-in principle-constructible"
R do_something(T&& t);

What we can see is, that functions (rather function specifications) are promising constructions (values) of a certain type. At this specification stage, we cannot be sure, that this is really the case. At the end we must also take a look on the implementation. The final question is - what can the compiler do for us also in the implementation area. But one after the other.

In C++-20 this construction allows us to work with universal references in a better way than before. But even this is an improvment, C++ is still not very educational with regards to mathematics. By using C++ a developer learns programming but not mathematics. I don't think that this is a must. I think this is a bad strategy.

All these things have to do with logic. With types and their interpretations together with a framework, which describes the relation between these basic objects, we make logic or something similar to logic. But the logical aspect should become more and more important.

So this is a vague description of what we are doing - or trying to do - here.

Polymorphic datatypes (sometimes known as Abstract Data Types - ADT) are closely related to the concept of a sum in category theory. But let's first take a look on the idea of a product.

A product is related to other objects, which also have projections. An object P has perhaps the projections

\(P_a: P \rightarrow A \qquad \hat{=} \qquad A^P \\ P_b: P \rightarrow B \qquad \hat{=} \qquad B^P\)

Our product has the projections

\((A \otimes B)_a: (A \otimes B) \rightarrow A \qquad \hat{=} \qquad A^{A \otimes B} \\ (A \otimes B)_b: (A \otimes B) \rightarrow B \qquad \hat{=} \qquad B^{A \otimes B}\)

If we have many of such objects P, our product is characterized by the property, that every P_a can be written as

\(P_a = (A \otimes B)_a \circ C_p\)

where

\(C_p: P \rightarrow (A \otimes B) \qquad \hat{=} \qquad (A \otimes B)^P\)

So the idea of all this is to say, that a product is a best representiation of the conecpt of projections. Th is allows us to say, that a product is a limit, which means exactly - something very good.

Now let's go the opposite direction, by reversing the arrows.

The opposite of an projection is an injection. Now we have two injections

\((A \oplus B)_a: A \rightarrow (A \oplus B) \qquad \hat{=} \qquad (A \oplus B)^A \\ (A \oplus B)_b: B \rightarrow (A \oplus B) \qquad \hat{=} \qquad (A \oplus B)^B\)

In analogy to the product every structure, which provides injections should be related to a sum via

\(I_a = C_s \circ (A \oplus B)_a\)

where

\(C_s: (A \oplus B) \rightarrow S \qquad \hat{=} \qquad S^{A \oplus B}\)

A sum is also called a coproduct because of the reverse arrow construction. As a coproduct, the limit property is also called colimit.

The main advantage of such a sum is that it represents many aspects by one aspect only. Comming back to the world of programming, such a common type is very useful as return type of a function. We can return a shape and this shape encapsulates perhaps a rectangle or a circle. We may automatically think on the object oriented programming feature inheritance. But I want to avoid the base class dependency. The base construction looks like

template<typename T>
struct data
{
   template<typename X>
   data(X&& x) : m_p(&x), m_i(tl_index_of<X,T>::value) {}

   template<typename F>
   decltype(auto) apply(F&& f)
   {
       return helper(fwd(f),T{},m_i);
   }

   template<typename F, typename L>
   decltype(auto) helper(F&& f, L l, std::size_t i)
   {
      if constexpr (std::is_same<L,typelist<>>::value) {
         throw 1;
      } else {
         if (i == 0) {
            auto p = static_cast<tl_first<L>*>(m_p)
            return f(p);
         }
         return helper(fwd(f),tl_tail<L>, i-1);
      }
   }

   void* m_p;
   const std::size_t m_i;
};

The sum type is represented by a typelist. The constructor saves the index of the injected type into a member. With this index we can reconstruct the real type and are able to apply the real type to the polymorphic function.

A little bit of test code demonstrates the principle.

template<typename>
struct obj
{
};

using objs = typelist<obj<circle>,obj<square>,obj<rectangle>>;

struct print;

template<>
struct fun<print>
{
   void operator()(obj<circle>*)
   {
      std::cout << "circle" << std::endl;
   }

   void operator()(obj<rectangle>*)
   {
      std::cout << "rectangle" << std::endl;
   }

   void operator()(obj<square>*)
   {
      std::cout << "square" << std::endl;
   }
};

int main()
{
   auto s = std::make_unique<obj<square>>();

   data<objs> o(s.get());

   o.apply(fun<print>());

   auto c = ctr<shape,circle>{3.5};
   return 0;
}

The next step is to connect the polymorphic data structure with the data constructors ctr in a more flexibel fashion. From the coding perspective this all looks very similar to the structures we find in the visitor pattern area. This is the one and only place I mention this pattern.

So let's improve this initial example of a polymorphic data type. A very flexible approach is to create a data carrier class together with a base class

namespace base
{
   struct carrier
   {
     carrier(std::size_t i) : index(i) {}
     const std::size_t index;
   };
}

namespace detail
{
   template<typename T>
   struct carrier : base::carrier
   {
     carrier(T&& _t) :
       base::carrier(ctr_index<clear_type<T>>),
       t(fwd(_t)) {}
     T t;
   };
}

Now let's align our first example

template<typename T, UQ_CTX(T)>
struct data
{
  template<typename X, UQ_CTX_CTR(T,X), UQ_CTX_COMPLETE(T)>
  data(X&& x) : c(new detail::carrier<X>{fwd(x)}) {}

  template<typename F>
  decltype(auto) apply(F&& f) const
  {
    return fwd(f) <op::d> *this;
  }

  template<typename F>
  decltype(auto) apply(F&& f)
  {
    return fwd(f) <op::d> *this;
  }

  std::unique_ptr<base::carrier> c;
};

I anticipated the introduction of an application operator op::d and I added three universal qualifiers. First, the data type parameter should reference a context

#define UQ_CTX(A_T) typename = ctx_types<A_T>

Second, the constructor parameter should represent a data constructor stucture, which references to the same context as the data parameter

template<typename C, typename T>
struct same_context : std::false_type {};

template<typename C, typename T>
struct same_context<C,ctr<C,T>> : std::true_type {};

template<typename C, typename T>
struct fun<same_context<C,T>>
{
  constexpr bool operator*()
  {
    return same_context<C,T>::value;
  }
};

#define UQ_CTX_CTR(A_T,A_X) typename = \
    typename std::enable_if<*fun<same_context<A_T,A_X>>()>::type

The last qualifier checks if all contructor objects can be constructed

namespace detail
{
  template<typename C, typename T>
  struct is_constructible;

  template<typename C, typename... T>
  struct is_constructible<C, typelist<T...>>
  {
    static constexpr bool value =
      (std::is_constructible<ctr<C,T>>::value && ...);
  };
}

template<typename C>
struct ctx_constructible
{
  static constexpr bool value =
    detail::is_constructible<C,ctx_types<C>>::value;
};

template<typename C>
struct fun<ctx_constructible<C>>
{
  constexpr bool operator*()
  {
    return ctx_constructible<C>::value;
  }
};

#define UQ_CTX_COMPLETE(A_T) typename = \
    typename std::enable_if<*fun<ctx_constructible<A_T>>()>::type

The cooresponding testcode is

int main()
{
  data<shape> o(ctr<shape,circle>{1.0});

  o.apply(fun<print>());

  return 0;
}

Bit isn't this polymorphic data type also a functor - better, can we deliver an functor interpretation for the function application?

Indeed, we can simply align the list functor code to

template<typename T, typename F>
struct fun<functor<data<T>>,F>
{
  F f; 

  using GL = ctx_types<T>;
  using GC = detail::carrier<ctr<T,util::tl_first<GL>,P...>>;
  using GR = decltype(f(std::declval<GC>().t));

  template<typename A>
  GR operator()(A&& a)
  {
    return apply(fwd(a),ctx_types<T>{},fwd(a).c->index);
  }

  template<typename A, typename L>
  GR apply(A&& a, L l, std::size_t i)
  {
    if constexpr (std::is_same<L,util::typelist<>>::value) {
      throw 1;
    } else {
      if (i == 0) {
        auto p =
          static_cast<carrier<ctr<T,util::tl_first<L>>>*>
          (fwd(a).c.get());
        return f(p->t);
      }
      return apply(fwd(a), util::tl_tail<L>{}, i-1);
    }
  }
};

Now the test code looks like this

int main()
{
  using namespace cat;

  data<shape> o(ctr<shape,circle>{1.0});

  fun<print>() <<op::fa>> o;

  return 0;
}

This application works, but is it really functorial? The problem is the return value. The return value is not of the type data<void>. The function fun<print> should translate the type data<shape> to a datatype data<void>. But the return value is simply void. Another function could be fun<perimeter>. Then the return value should be data<double>, but we will get simply double as the return value.

Actually, we can say, that the application mechanism for the data objects is similar to functorial data, but not exactly the same. One measure to distinguish this situation from functorial data, could be to introduce a new operator.

namespace op
{
    const struct a_t {} a;
    const struct fa_t {} fa;
    const struct da_t {} da;

    template<typename C, typename V>
    struct capture
    {
       V v;
    };
}

The operator definitions must be aware of this type

template<typename F, typename G>
decltype(auto) operator>>(F&& f, G&& g)
{
  if constexpr (is_op<op::a_t,F>) {
    return fwd(f).v(fwd(g));
  }
  if constexpr (is_op<op::fa_t,F>) {
     return functor<util::clear_type<G>>()(fwd(f).v)(fwd(g));
  }
  if constexpr (is_op<op::da_t,F>) {
     return data_application<util::clear_type<G>>()(fwd(f).v)(fwd(g));
  }
  throw 1;
}

Missing is the new concept data_application. Again, technically it's something like the functor concept

template<typename T>
struct functor
{
  template<typename F>
  constexpr decltype(auto) operator()(F&& f) const
  {
    return fun<functor<util::clear_type<T>>,F>{fwd(f)};
  }
};

template<typename T>
struct data_application
{
  template<typename F>
  constexpr decltype(auto) operator()(F&& f) const
  {
    return fun<data_application<util::clear_type<T>,F>{fwd(f)};
  }
};

The plugin code needs now only a new creation strategy

template<typename T, typename F>
struct fun<data_application<data<T>>,F>
{
  F f;

  using GL = ctx_types<T>;
  using GC = detail::carrier<ctr<T,util::tl_first<GL>,P...>>;
  using GR = decltype(f(std::declval<GC>().t));

  template<typename A>
  GR operator()(A&& a)
  {
    return apply(fwd(a),ctx_types<T>{},fwd(a).c->index);
  }

  template<typename A, typename L>
  GR apply(A&& a, L l, std::size_t i)
  {
    if constexpr (std::is_same<L,util::typelist<>>::value) {
      throw 1;
    } else {
      if (i == 0) {
        auto p =
          static_cast<carrier<ctr<T,util::tl_first<L>>>*>
          (fwd(a).c.get());
        return f(p->t);
      }
      return apply(fwd(a), util::tl_tail<L>{}, i-1);
    }
  }
};

We can now apply a polymorphic function directly to the data object

auto data<shape> o(ctr<shape,circle>{2.2});

auto value = fun<perimeter>() <<op::da>> o;

With a small extension of the perimeter function

template<>
struct fun<perimeter>
{
  double operator()(const data<shape>& d)
  {
    return (*this) <<op::da>> d;
  }
  ...
};  

we can directly apply the function to the data

auto data<shape> o(ctr<shape,circle>{2.2});

auto value = fun<perimeter>() <<op::a>> o;

A further concept comes now, which is widely used in the area of operations with side effects. A operation may return something or nothing dependent on the behaviour of the technical behaviour of the environment. Of interest is especially the chaining of such operations.

The polymorphic data concept represents an opaque data approach like it is used typically in the area of C programming. The implementation of the constructors can be completely placed in implementation files.

Object oriented programming motivates the developer to define data in headers together with the functions to work with this data. But data my have many dependencies and these dependencies are spread over the software via the headers.

Sure, this can be avoided. One way is to use abstract interfaces and object factories, so that the concrete classes and factory implementations can be placed in implementation files.

In the object oriented context the question may arise, that why we should deliver an abstraction if we have only one candidate of realization.

The answer is, that abstraction has here also the purpose to hide the concrete data in implementation files. But is this the right way to go to achive data hiding?

Object oriented inheritance abstraction is not available for C developers. But even so, also C developers have the wish to hide away the concrete data from the user of an interface. As an example let's assume we want connect to a database MyDb. So we can do it in the following way

struct MyDbConnection;

MyDbConnection* MyDbConnect(char* connection_string);
void MyDbDisconnect(MyDbConnection* connection);

int main()
{
  MyDbConnection* c = MyDbConnect("hostname:port:dbname:username:password");

  MyDbDisconnect(c);

  return 0;
}

As a C++ developer I would expect, that the MyDbConnection pointer points to a MyDbConnection structure. But this must not be the case as the following implementation code shows

MyDbConnection* MyDbConnect(char* connection_string)
{
  internal_connection* ic;

  ic = internal_connect(connection_string);

  return (MyDbConnection*)ic;
}

void MyDbDisconnect(MyDbConnection* c)
{
  internal_connection* ic;

  ic = (internal_connection*)c;

  internal_disconnect(ic);
}

So the physical meaning of MyDbConnection can be anything. It's only an interpretation. We may say it is a connection handle. But if we switch back into the object oriented context we may think, that we must use inheritance to solve this problem. This way a more or less complex theory can be the result. But is this simple technical aspect really a spohisticated abstraction mechanism.

Monads are often mentioned in functional programming in the area of side-effect-ful operations. They are useful for it, but the meaning behind hasn't anything to do with side-effects. In the same sense a std::optional can be used to handle side-effects but that's not the nature of a std::optional. A std::optional may have one value or not. If it has a value, we can take this value as input for a function, which itself returns a std::optional - containing a value or not. In the context of operations with side effects this behaviour may be useful.

Containing a value or not is like a list, which can contain at most 1 element. So it is not a surprise, that there must exist a functor interpretation for a std::optional - only the capture helper must be implemented

template<typename T, typename F>
struct fun<functor<std::optional<T>>,F>
{
  template<typename A>
  decltype(auto) operator()(A&& a)
  {
    using type =
      decltype(f(std::declval<decltype(*a)>()));

    if constexpr (std::is_same<type,void>::value) {

      if (fwd(a)) {
        f(*fwd(a));
      }

    } else {

      std::optional<type> ro;

      if (fwd(a)) {
        ro = f(*fwd(a));
      }

      return ro;
    }
  }

  F f; 
};

In contrast to a normal functor situation, let's consider another function type:

\( f: A \rightarrow std::optional \langle B \rangle \)

If we take for \(A\) an \(int\) and for \(B\) a \(double\) the functor way would deliver

std::optional<std::optional<double>>
test(std::optional<int> o,
     std::function<std::optional<double>(int)> f)
{
   std::optional<std::optional<double>> r;

   if (o) {
      r = f(*o);
   } 
   return r;
}

The functor operation would return an std::optional<std::optional<double>>. It's clear, a std::optional<double> would carry enough information. But before we start now to implement a sophisticated template deduction algorithm, to solve this problem, it's worth to show, that the nested std::optional construction represents a binary product. This is a nice example, which tells something about abstraction in category theory. Let's take a look on the following pattern sequence

\( optional \langle optional \langle int \rangle \rangle \qquad \hat{=} \qquad optional(optional(int)) \)

Here I'm replacing angle brackets by round brackets. Now it looks now like a composition

\( optional(optional(int)) \qquad \hat{=} \qquad (optional \circ optional)(int) \)

And as a shortcut we can write

\( (optional \circ optional)(int) \qquad \hat{=} \qquad optional^2(int) \)

Now take a look on a list and a optional or more in general on a G and on a H

\( G \circ H \)

Next we can define the projections

\( first(G \circ H) = G \)

and

\( second(G \circ H) = H \)

Because of the projections we can say \( G \circ H \) is a binary product. But the \(\circ\) is perhaps distracting. We can also write

\( (G,H) \qquad \hat{=} \qquad G(H(type)) \qquad \hat{=} \qquad G \langle H \langle type \rangle \rangle \)

Now let's again consider the composition of the identical type constructors or type functions

\( G \circ G \)

The question is now, if there exists an operation \(\mu\), which holds

\( \mu: G \circ G \rightarrow G \)

Such a μ we can find on values very often

\( (string, string) \rightarrow string \)

is just a string concatenation and

\( (int,int) \rightarrow int \)

can be expressed by an addition or a multiplication.

The μ is the essence of a structure, which is called a monoid.

In the case, such a μ exists for type constructors or type functions like an optional or a list, we can define the monadic binding

\( G \langle A \rangle \rightarrow ( A \rightarrow G \langle B \rangle ) \rightarrow G \langle B \rangle \)

Such a G can be regarded as a monad, which itself can be regarded in a certain context as a monoid.

From the programmer perspective the task is now to deliver a new operator and the monadic binding. For the structurs optional and list we have already functor interpretations. For both structures also an interpretation of a monad is possible.

The monad interpretation looks identical compared to the functor one

template<typename T>
struct functor
{
  template<typename F>
  constexpr decltype(auto) operator()(F&& f) const
  {
    return fun<functor<util::clear_type<T>>,F>{fwd(f)};
  }
};

template<typename T>
struct monad
{
  template<typename F>
  constexpr decltype(auto) operator()(F&& f) const
  {
    return fun<monad<util::clear_type<T>>,F>{fwd(f)};
  }
};

Next we can introduce a monadic operator type

namespace op
{
   const struct a_t {} a;
   const struct fa_t {} fa;
   const struct da_t {} da;
   const struct ma_t {} ma;

   template<typename C, typename V>
   struct capture
   {
      V v;
   };
}

The closing part of the operator can now be written as

template<typename F, typename G>
decltype(auto) operator>>(F&& f, G&& g)
{
  if constexpr (is_op<op::a_t,F>) {
    return fwd(f).v(fwd(g));
  }
  if constexpr (is_op<op::fa_t,F>) {
     return functor<util::clear_type<G>>()(fwd(f).v)(fwd(g));
  }
  if constexpr (is_op<op::da_t,F>) {
     return data_application<util::clear_type<G>>()(fwd(f).v)(fwd(g));
  }
  if constexpr (is_op<op::ma_t,F>) {
     return monad<util::clear_type<G>>()(fwd(f).v)(fwd(g));
  }
  throw 1;
}

An example for a monad function can be that of an optional

template<typename T, typename F>
struct fun<monad<std::optional<T>>,F>
{
  template<typename A>
  decltype(auto) operator()(A&& a)
  {
    using type =
      decltype(f(std::declval<decltype(*a)>()));

    if constexpr (std::is_same<type,void>::value) {

      if (fwd(a)) {
        f(*fwd(a));
      }

    } else {

      type ro;

      if (fwd(a)) {
        ro = f(*fwd(a));
      }
      return ro;
    }
  }

  F f; 
};

A test for this monad could be

using namespace cat;

std::optional<double> test_optional_functor(std::optional<int> o)
{
  auto one_third = [] (int e) {
    return std::optional<double>(e*0.33333);
  };

  return one_third <<op::ma>> o;
}

int main()
{
  auto o = test_optional_functor({1});

  if (o) {
    std::cout << *o << std::endl;
  }

  return 0;
}

This situation describes a monadic application, where a monadic function is applied to a monadic value. A monadic binding goes the opposite direction, which takes a monadic value and binds it to a monadic function. This can be achieved simply by switching the parameters around. The monadic binding is often used to simulate the procedural left to right sequencing of commands. Here the actual functor code motivates the go first the analog application way.

Another problem we have still regarding the use of operators. We don't have control over the operator precedence. A right to the left logic is easier to implement, than a left to right sequencing.

Actually we can apply a function on a value

fun<x>() <<op::a>> v;

But what can we do if the function has more than one parameter in it's definition. We should be able to write the following

f<x>() <<op::a>> v1 <<op::a>> v2;

To deliver such a functionality let's first introduce a new operator

namespace cat::op
{
  struct t_ta ta;
}

Now we can plugin a new concept - the function transpose - according to the considerations in an earlier section. A function transpose is perhaps not the same as a curried function, because the transposed function is not equal compared to the original one - in c++.

The transpose of a function is again a function, where values are captured. Again, the term capture of a lambda is equivalent to members of an object. So a transpose function could be

struct transpose {};

template<typename F, typename A>
struct fun<transpose, F ,A>
{
  fun(F&& _f, A&& _a, transpose) : f(fwd(_f)), a(fwd(_a)) {}

  template<typename... X>
  constexpr decltype(auto) operator()(X&&... x)
  {
    return f(a,fwd(x)...);
  }

  F f;
  A a;
};

template<typename F, typename A>
fun(F&&,A&&,transpose) -> fun<transpose,F,A>;

The operator handler can now return this function in the following way

template<typename F, typename G>
decltype(auto) operator>>(F&& f, G&& g)
{
  if constexpr (is_op<op::a_t,F>) {
    return fwd(f).v(fwd(g));
  }
  if constexpr (is_op<op::t_ta,F>) {
    return fun(fwd(f).v,fwd(g),transpose{});
  }
  if constexpr (is_op<op::fa_t,F>) {
    return functor<util::clear_type<G>>()(fwd(f).v)(fwd(g));
  }
  if constexpr (is_op<op::da_t,F>) {
    return data_application<util::clear_type<G>>()(fwd(f).v)(fwd(g));
  }
  if constexpr (is_op<op::ma_t,F>) {
    return monad<util::clear_type<G>>()(fwd(f).v)(fwd(g));
  }
  throw 1;
}

A test code could loo like this

int test_transpose_1()
{
  auto multi = [] (int e, int f) {
    return e*f;
  };

  using namespace cat;

  return multi <<op::ta>> 6 <<op::a>> 2;
}

int test_transpose_2()
{
  auto multi = [] (int e, int f) {
    return e*f;
  };

  using namespace cat;

  return (multi <<op::ta>> 6 <<op::ta>> 2)();
}

int main()
{
  auto r1 = test_transpose_1();

  std::cout << r1 << std::endl;

  auto r2 = test_transpose_2();

  std::cout << r2 << std::endl;

  return 0;
}

We can improve this construction by separating the transpose function by an transpose operator and an application

template<typename F>
constexpr decltype(auto) operator~(F&& f)
{
  return fun(fwd(f),name::transpose{});
}

The closing operator part can now be rewriten as

template<typename F, typename G>
decltype(auto) operator>(F&& f, G&& g)
{
  ...
  if constexpr (is_op<op::ta_t,F>) {
    return (~fwd(f).v) <<op::a>> fwd(g);
  }
  ...
}

We can add some additional testcases, which show the usage of this operator

int test_transpose_1()
{
  using namespace cat;

  auto multi = +[] (int e, int f) {
    return e*f;
  };

  return (~multi) <<op::a>> 6 <<op::a>> 2;
}

int test_transpose_2()
{
  using namespace cat;

  auto multi = +[] (int e, int f) {
    return e*f;
  };

  return (~(~multi <<op::a>> 6) <<op::a>> 2)();
}

int test_transpose_3()
{
  using namespace cat;

  auto multi = +[] (int e, int f) {
    return e*f;
  };

  return (multi <<op::ta>> 6 <<op::ta>> 4)();
}

The transpose operator ~ and the lambda operator + seem to me to be very powerful helpers, which avoid very lengthy function calls. This is the way operators should work in general.

Now we can regard a functor operation, where we apply a binary function on a list of values. The result will be a list of unary functions, which we want apply again to a list of values. This consideration leads to the concept of an applicative. This concept lies between the functor and the monad. So an applicative is a functor but not a monad. A monad is an applicative.

The concept of an applicative can be motivated by applying a binary function to an encapsulated value. In the case of a list we apply such a function to each list element. Let's assume we take the list elements as the first argument of this binary function. The result is a list of unary functions. Now we come in the situation, that we want - perhaps - apply this list of functions to another list of values. So the applicative generalizes the functor. So let's first construct such a list of functions

auto lf = [](int a, int b) { return a+b;} <<op::fta>> list<int>{1,2,3};

The next step is now to specify an operator aa, which expresses this application type

auto l = lf <<op::aa>> std::list<int>{5,6,7};

In the case of a list, every function of the function list, will be applyed to the list of values, like the functor algorithm would do.

In the same way we integrated the functor or the monad concept, the applicative can also be integrated in the same way via the new operator aa.

The code can be found in the source code repo.

Let's assume, that we are only working with function of one argument. If we compose two such functions f and g using the composition operator \(\circ\)

\( f \circ g \)

we translate the argument of the function f from A to B, if g takes a parameter of type B and creates a value of type A. If we use the exponential style for functions we get

\( f:X^A \xrightarrow{g:A^B} f':X^B \)

So the argument type movement goes for the functions f and f' from A to B, but the arugment transforming function g moves from B to A. These opposite directions indicate a contravariant functor. This seems to be the nature of a composition.

But is it possible to look on the composition as a covariant functor? For this purpose we can regard the function f as a transformation of the return type of function g

\( g:A^B \xrightarrow{f:X^A} g':X^B \)

Now the return type movement of g goes from A to X as it goes for the return type transforming function f. So we are now able to use a covariant functor to model a composition.

Now we can provide a functor plugin for a fun object in the following way

namespace cat
{
  template<typename F, typename... T>
  struct fun<name::functor,fun<T...>, name::application>, F>
  {
    template<typename G>
    decltype(auto) operator()(G&& g)
    {
      return [gg=fwd(g),ff=std::move(f)](auto&&... a) mutable {
        return ff(gg(fwd(a)...));
      };
    }

    F f; 
  };
}

The composition is simply a functor application, where the one function translates the return value of the other one

double test_fun_functor()
{
  using namespace cat;

  auto multi = +[](int a, int b) {
    return a * b;
  };

  auto one_third = +[] (int e) {
    return e*0.33333;
  };

  return (one_third <op::fa> multi)(4,6);
}

int main()
{
  std::cout << test_fun_functor() << std::endl;

  return 0;
}

Instead of a fun-functor we can identify this functor to be a hom-functor in category theory. We can extend a little bit this composition approach by a transpose aspect. Let's take a look on the testcode first

double test_fun_functor_transpose()
{
  using namespace cat;

  auto multi = +[](int a, int b) {
    return a * b;
  };

  return (multi <op::fta> multi)(4,6)(2);
}

int main()
{
  std::cout << test_fun_functor_transpose() << std::endl;

  return 0;
}

The result of the composition is again a function, which takes additional arguments. We can state, that the result of a composition is an exponential transpose of the first argument. This transpose may need additional parameters to complete the call. The plugin code is very simple. First the operator definition

    const struct a_t {} a;
    const struct ta_t {} ta;
    const struct fa_t {} fa;
    const struct fta_t {} fta;
    const struct da_t {} da;
    const struct ma_t {} ma;

    struct capture
    {
      V v;
    };
}

This defines a new operator symbol fta, which is connected within the close operator implementation

template<typename F, typename G>
decltype(auto) operator>(F&& f, G&& g)
{
  ...
  if constexpr (is_op<op::fta_t,F>) {
    using ftype = decltype(fwd(f).v);
    return functor<util::clear_type<G>,
                   name::transpose,ftype>{fwd(f).v}(fwd(g));
  }
  ...
}

Finally the plugin code

template<typename F, typename... T>
struct fun<name::functor,fun<T...>, name::transpose, F>
{
  template<typename G>
  constexpr decltype(auto) operator()(G&& g) const
  {
    return +[gg=fwd(g),ff=std::move(f)](auto&&... a) {
      return +[fff=std::move(ff),
               ggg=std::move(gg),
               t=std::forward_as_tuple(a...)](auto&&... b)
      {
        return fff(std::apply(ggg,t),fwd(b)...);
      };
    };
  }

  F f; 
};

As a first example of a polimorphic data type we can replace a std::optional by the maybe type. Two data constructors are needed - a constructor, which represents nothing and a constructor to represent just the value.

namespace cat
{
  namespace name
  {
    struct maybe {};
    struct nothing;
    struct just;
  }

  template<>
  struct ctx<name::maybe>
  {
    using types = typelist<name::just,name::nothing>;
  };

  template<typename A>
  struct ctr<name::maybe,name::nothing,A>
  {};

  template<typename A>
  using nothing = ctr<name::maybe,name::nothing,A>;

  template<typename A>
  struct ctr<name::maybe,name::just,A>
  {
    ctr(A&& a) : value(fwd(a)) {}

    A value;
  };

  template<typename A>
  using just = ctr<name::maybe,name::just,A>;

  template<typename A>
  using maybe = data<name::maybe,A>;
}

The functor, applicative and monad interpretations must now be added to this structure, by using the data application operator. Take a look at the code for more details.

A possible list implementation looks very similar.

In analogy to the maybe structure, we need to data constructures. First one, which represetns an empty list and second one, which holds the list_data.

namespace cat
{
  namespace name
  {
    struct list {};
    struct list_data;
    struct empty;
  }

  template<>
  struct ctx<name::list>
  {
    using types = typelist<name::empty,name::list_data>;
  };

  template<typename A>
  struct ctr<name::list,name::empty,A>
  {};

  template<typename A>
  using empty = ctr<name::list,name::empty,A>;

  template<typename A>
  struct ctr<name::list,name::list_data,A>
  {
    template<typename X>
    ctr(A&& a, X&& x) : first(fwd(a)), tail(fwd(x)) {}

    A first;

    data<name::list,A> tail;
  };

  template<typename A>
  using list_data = ctr<name::list,name::list_data,A>;

  template<typename A>
  using list = data<name::list,A>;
}

In contrast to the maybe structure, the list_data object has an additional tail attribute, which makes this structure recursive. The recursion ends with an empty list. Again we have to add the functor, applicative and the monad interpretation to this structure. For details refer to the code.

In functional languages all values are constant. So if we want to develop a language with similar properties it may be obvious always copying data. On the other hand functional languages deal with performance problems by using caching strategies in the background. Another approch was motivated by J.-Y. Girard with his work on linar logic, which suggested a new type system called linear types. Linear types promise to get rid of garbage collection strategies by using effective resource usage strategies directly in the functional code.

In c++ we come from the opposite side. Working with resources like memory allocation and deallocation - is very central topic for a c++ developer connected with the permamnent fear to make mistakes in this area. Newer concepts like unique - or smart pointers promise to solve problems in this area if used consequently.

In contrast to c++, linear types is a language concept. This means, that mistakes in using resources is recognized at compiletime - it's a logical problem.

To show some awareness for this situation I want to introduce a polymorphic value datatype, which can hold a reference to the data or the data itself. The idea behind is to copy data only if there is a logical requirement. In all other situations data should be moved or referenced. Currently I want to avoid data copies. So let's start with list values:

namespace cat
{
  namespace name
  {
    struct value;
    struct rvalue;
    struct lvalue;
  }

  template<>
  struct ctx<name::value>
  {
    using types = typelist<name::rvalue,name::lvalue>;
  };

  template<typename A>
  struct ctr<name::value,name::lvalue,A>
  {
    A& value;
  };

  template<typename A>
  struct ctr<name::value,name::rvalue,A>
  {
    A value;
  };

  template<typename A>
  using value = data<name::value,A>;
}

For this change a getter and a creator are making the work easier

namespace cat
{
  namespace name
  {
    struct create;
    struct get;
  }

  template<>
  struct fun<name::value,name::create>
  {
    template<typename A>
    constexpr value<A> operator()(A&& a) const
    {
      if constexpr (std::is_rvalue_reference<A&&>::value) {
        return rvalue<A>(fwd(a));
      } else {
        return lvalue<A>(fwd(a));
      }
    }
  };

  constexpr auto value_create = fun<name::value,name::create>();

  template<>
  struct fun<name::value,name::get>
  {
    template<typename X>
    requires Value<X>
    constexpr decltype(auto) operator()(X&& x) const
    {
      return (*this) <<op::da>> fwd(x);
    }

    template<typename D>
    requires RValue<D>
    constexpr auto operator()(D&& d) const -> decltype(d.value)&
    {
      return fwd(d).value;
    }

    template<typename D>
    requires LValue<D>
    constexpr auto operator()(D&& d) const -> decltype(d.value)
    {
      return fwd(d).value;
    }
  };

  constexpr auto value_get = fun<name::value,name::get>();

In cases in which values cannot be moved we need a copy:

template<>
struct fun<name::value,name::copy>
{
  template<typename X>
  requires Value<X>
  constexpr util::tp<X> operator()(X&& x) const
  {
    return (*this) <<op::da>> fwd(x);
  }

  template<typename X>
  requires LValue<X>
  constexpr value<vt<X>> operator()(X&& x) const
  {
    return util::tp<X>(fwd(x).value);
  }

  template<typename X>
  requires RValue<X>
  constexpr value<vt<X>> operator()(X&& x) const
  {
    return lvalue<vt<X>>(fwd(x).value);
  }
};

So a value copy translates rvalues into lvalues - in terms of constructors. For such a value construction a functor interpretation can be provided. If we then would use a value of a list, we would get a nested functor. So working with values makes the whole topic much more complicated. It's a good test to see how stable the codegeneration works.

For details refer to the code repository.

Now we can study the resource management by introducing some list operations like filter and quicksort. Beside the resource management aspect, the recursive structure is of high interest. The recursive structure shows on one look the relation between the big picture and the structural details.

At this point it's not so clear if the language developed here will be simple enough for the end user. The way to go is still long.

An OO developer may ask why should I introduce a base class abstraction if I have only have one class. The answer is, to hide the data structure from the client. The client should use functions not server data or implementation data. In practice it means, that we can put implementation data structures into the imlementation files (or into private header files). So we will not distribute data structures by the use of (public) header files.

C programmers are doing the same with opaque pointers. They have in common with functional languages, that they do not need inheritance.

The concept of an ADT or a sum type can be easily expanded to the one of an Generalized Abstract Data Type. To achive this generalization the list of allowed contructors must depend on the type parameter. Then we have an ADT if for all type parameters we get the same list of constructors. At this stage I only document the idea. The change of the code is not very complicated and is avaialble via the code repository.

Actually we have basic constructions like ctx, ctr, data, fun. But we are able to use a central structure obj to define all these types by name.

Because of the flat structure of the code - especially of the data construction - creating a subtype (inheritance) may help in some situations to simplify the usage. This way we can define appropriate constructor deduction helpers. For this purpose I chenged the code to provide this. But it is not essential.

The example code can be found at http://git.macajobe.de.

For making a runnable program take a look at the README.

The main intension of all this work is not to motivate functional programming. The main intension is to get more and more a feeling how to use a formal language to make proofs. If something is proofed, it must not be tested - in principle.

Important is, that complex proofs may depend on less complex proofs. So a proof must in general be stable. It must be possible to rely on it. A proof must always be valid, not only sometimes. But computing cannot live without the sometimes effect. So the art of programming is first to separate the sometimes world from the stable world and second to increase more and more the stable world.

From this point of view we can sepcify requirements on the programming language - or better - the programming paradigma to use. I would say, without a proof, that the functional paradigma is better suited to solve the provability requirements.

It's a long way to get a complete understanding how proofing works using a formal language. But this means, that functional languages deliver a long term learning environment, which is not given in the same way as in an imperative programming world. Even it's very likely, that functional programmers should also write better programs with an imperative language than imperative purists.

I'm not sure if the introduction of functional concepts into the imperative programming world makes the imperative programmers thinking functional. Functional concepts in imperative programming languages are perhaps more features and a motivation for experiments, than a motivation to change the way of thinking.

There is certainly a big community, which is very impressed by the topic programming. Even it should be possible to learn children how to write or create software – is the opinion. Why there isn't an equivalent community, which states, that children should learn mathematics (perhaps there is one I don't know)? Programming seems to be much simpler, could be an answer. Or, programming is much more exiting?

In the same direction goes the evolution of getting more and more programming languages. It seems, there are many problems, which can only be solved by programming.

Another aspect is the device – the computer, the smartphone – which seems to be an object of desire and the language to talk with are programming languages.

If I talk in this way about programming, the feeling must arise, that something is missing. The question is "why".

One direct answer on my own question "why" is, that programmiing let us feel to make important things, because we are using a language in a formalized, systemtic way, which give us the impression it has to do with logic. So we feel like mathematicians.

Indeed, there is a connection between programming and logic. But in the end our feeling is in general wrong.

But what are the indicators of this failure. I think it is expressed in the yearning after new programming languages, new language features and new language concepts. Even I am a highly experienced c++ developer – and I can say it's a complex language – not so easy to manage – what is the result of my logical work. What is the logic of my matheamical work my soul feels to do.

Devices are all around. So children will become good pyhsicists, because of the experiences they make in the area if doing something and analyzing the response. In the same way software developers are making code and they only know if it is working correctly by testing. Without testing we cannot be sure.

But logic in a mathematical sense is more art then physics. And art must be exchanged by people and certainly not by devices.

Mathematics is only one element in the world of the art of thinking systematically. Philosophy and Linguistic as scientific research areas are in the same way important. So if you are bored - take a look on these disciplines in the area of logic.

If we would argue, can we really distinguish devices from human beeings and is my last statement really acceptable I would say.

We are able to construct a world where it will be difficult to distinguish devices from a human beeings but we can also do the opposite.

In a world in which it is difficult to know if an intelligence is of human nature or not, it should be alway possible to identify the origin of an intelligence, because of the creation path - something like a birth certificate. I ignore my personal fellings at this point. That's a different thing.

Now, is it possible, that a human beeing can construct a device, which is more intelligence than a human beeing. Because the term intelligence is not a very clear term - the meaning is not totally clear - we can be more precise.

Is it possible, that a human beeing can construct a device, which has more capabilities in logic than the creator?

But if there is an intelligence of an higher order, it would not be possible for human beeings to prove, that this is really the case. This means that this intelligence is potentially bullshit. I cannot prove that something is correct but I don't understand it.

So what is the motivation to find such an intelligence. It's a way to introduce god. And there is no way to dicuss about god. On one hand god is dead, so take the new one.

Lectures on functional analysis are talking about fuunctions as they would be data. The idea is simple. If we can find function vector spaces, there is not so much a difference compared to ordinary vector spaces. In the speech of functional programming, functions are first class objects. In functional analysis a function must have a length - a norm. And a norm defines a distance. In c++ we can say, that an object is a struct and a function object has call operators and data object has members. Even c++ has a strange strategy in using terms and notions in the area of meta programming, it's perhaps of interest, that both concepts - function and data - can be derived from a struct. Yes, the class thing is not so must of interest.

• https://gist.github.com/sorrge/2d2271e57ad1e91a50ea Dependent types in C++
• https://web.mit.edu/6.001/6.037/sicp.pdf Structure and Interpretation of Computer Programs
• https://vittorioromeo.info/index/blog/capturing_perfectly_forwarded_objects_in_lambdas.html
• https://awodey.github.io/catlog/notes/catlog0.pdf
• https://www.cs.bu.edu/~hwxi/atslangweb/

Matthias Wolff 8008 Zuerich CH Im Walder 14